
从集合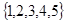 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.
①记性质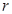 :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质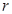 的概率;
的概率;
②记所取出的非空子集的元素个数为 ,求
,求 的分布列和数学期望
的分布列和数学期望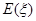 .
.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:江西省重点中学盟校2010届高三第二次联考理科试题 题型:解答题
(本小题满分12分)
从集合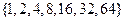 的所有非空真子集中等可能地取出一个.
的所有非空真子集中等可能地取出一个.
(1)求所取的子集中元素从小到大排列成等 比数列的概率;
比数列的概率;
(2)记所取出的子集的元素个数为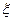 ,求
,求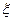 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省、岳阳县一中高三11月联考文科数学 题型:填空题
已知集合 为非空集合,且
为非空集合,且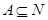 ,定义
,定义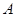 的“交替和”如下:将集合
的“交替和”如下:将集合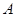 中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合
中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合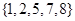 的交替和为8-7+5-2+1=5,集合
的交替和为8-7+5-2+1=5,集合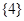 的交替和为4,当
的交替和为4,当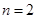 时,集合
时,集合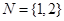 的非空子集为
的非空子集为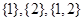 ,记三个集合的交替和的总和为
,记三个集合的交替和的总和为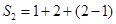 = 4,则
= 4,则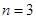 时,集合
时,集合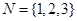 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和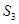 =
;集合
=
;集合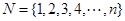 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和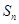 =
=
查看答案和解析>>
科目:高中数学 来源:2012届湖南省澧县一中、岳阳县一中高三11月联考文科数学 题型:填空题
已知集合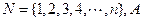 为非空集合,且
为非空集合,且 ,定义
,定义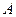 的“交替和”如下:将集合
的“交替和”如下:将集合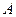 中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合
中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合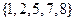 的交替和为8-7+5-2+1=5,集合
的交替和为8-7+5-2+1=5,集合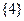 的交替和为4,当
的交替和为4,当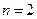 时,集合
时,集合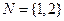 的非空子集为
的非空子集为 ,记三个集合的交替和的总和为
,记三个集合的交替和的总和为 = 4,则
= 4,则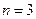 时,集合
时,集合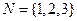 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和 = ;集合
= ;集合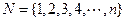 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和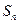 =
=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com