
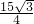 ,AB=3,AC=5,且角A为钝角,边BC的中点为D,则AD长度为
,AB=3,AC=5,且角A为钝角,边BC的中点为D,则AD长度为
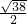

 ,再由角A为钝角,可得A=
,再由角A为钝角,可得A= .△ABC中,由余弦定理求得BC=7,再由正弦定理求得sinB的值.由题意可得B为锐角,利用同角三角函数的
.△ABC中,由余弦定理求得BC=7,再由正弦定理求得sinB的值.由题意可得B为锐角,利用同角三角函数的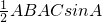 =
=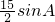 =
=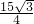 ,∴sinA=
,∴sinA= .
. .
. =49,∴BC=2BD=7.
=49,∴BC=2BD=7.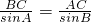 ,即
,即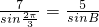 ,∴sinB=
,∴sinB=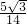 .
.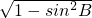 =
= .
.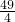 -21•
-21• =
= ,∴AD=
,∴AD= ,
,

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com