练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
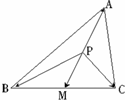
    （1）△ABC中，P为中线AM上一点，|
    AM
    |=4    ，设
    AP
    =2
    PM
    ，试用
    AB
    ，
    AC
    表示
    PA
    ；
    （2）求
    PA
    •(
    PB
    +
    PC
    )    的最小值．
    分析：易得M是BC的中点，P是三角形ABC的重心，进而得
    PA
    •(
    PB
    +
    PC
    )    =
    PA
    •2
    PM
    ，由数量积的定义可得答案．
    解答：解：（Ⅰ）由于 
    PA
    =-
    AP
    =-
    2
    3
    AM
    =-
    2
    3
    •
    1
    2
    (
    AB
    +
    AC
    )
    则
    PA
    =-
    1
    3
    (
    AB
    +
    AC
    )
    （Ⅱ）在△PBC中，M为BC的中点，∴
    PM
    =
    1
    2
    (
    PB
    +
    PC
    )
    设|
    PA
    |=x        
    则
    PA•
    (
    PA
    +
    PC
    )=2
    PA
    •
    PM
    =2|
    PA
    |•|
    PM
    |•cosπ    =-2x•（4-x）=2x2-8x
    当x=2时，函数最小值为-8
    点评：本题考查向量加减混合运算及几何意义，属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    指出下列各组命题中，p是q的什么条件(在“充分而不必要条件”，“必要而不充分条件”，“充要条件”，“既不充分又不必要条件”中选出一种作答)．

    (1)在△ABC中，p：A＞B，q：BC＞AC；

    (2)对于实数x，y，p：x＋y≠8，q：x≠2或y≠6；

    (3)在△ABC中，p：sinA＞sinB，q：tanA＞tanB；

    (4)已知x，y∈R，p：(x－1)2＋(y－2)2＝0，q：(x－1)(y－2)＝0．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    指出下列各组命题中，p是q的什么条件？(在“充分而不必要条件”“必要而不充分条件”“充要条件”“既不充分也不必要条件”中选出一种)

    (1)在△ABC中，p：∠A＞∠B，q：BC＞AC；

    (2)p：a＝3，q：(a＋2)(a－3)＝0；

    (3)p：a＞2，q：a＞5；

    (4)p：a＜b，q：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    指出下列各组命题中，p是q的什么条件？（在“充分而不必要条件”“必要而不充分条件”“充要条件”“既不充分也不必要条件”中选出一种）

    (1)在△ABC中，p:∠A＞∠B,q:BC＞AC;

    (2)p:a=3,q:(a+2)(a-3)=0;

    (3)p:a＞2,q:a＞5;

    (4)p:a＜b,q:＜1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    指出下列各组命题中，p是q的什么条件？

    (1)在△ABC中，p：A＞B，q：BC＞AC；

    (2)p：a=3，q：(a+2)(a-3)=0；

    (3)p：a＜b，q：＜1.

    查看答案和解析>>

    同步练习册答案