
 如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以100
如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以100| 6 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 6 |
| 3 |
| 2 |
| 6 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 6 |


科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌二中高一(下)第一次月考数学试卷(解析版) 题型:解答题
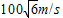 沿直线OO′飞行,并在O位置时测得∠BAO=75°,∠ABO=60°.雷达继续跟踪此飞行物,经过1.5min 后,飞行物到达O′,并 测得∠BAO′=30°,∠ABO′=120°,求两雷达观察站A和B之间距离a的大小.
沿直线OO′飞行,并在O位置时测得∠BAO=75°,∠ABO=60°.雷达继续跟踪此飞行物,经过1.5min 后,飞行物到达O′,并 测得∠BAO′=30°,∠ABO′=120°,求两雷达观察站A和B之间距离a的大小.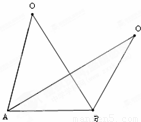
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com