Question

已知：双曲线的顶点坐标(0，1)，(0,-l)，离心率，又抛物线的焦点与双曲线一个焦点重合．

(1)求抛物线的方程；

(2)已知是轴上的两点，过做直线与抛物线交于两点，试证:直线与轴所成的锐角相等．

(3)在(2)的前提下，若直线的斜率为1，问的面积是否有最大值?若有，求出最大值．若没有，说明理由．

Answer 1

(1) (2)略

解析:

(1)由题意,设双曲线方程为,则解得  ------2分

所以双曲线两焦点为,即故,

∴抛物线的方程为;-----------------5分

(2)设直线AB方程为,代入抛物线的方程为得:

,

设,,则,  -----------------7分

要证直线与轴所成的锐角相等,只证明,

∵=,

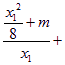
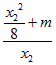所以原命题成立.-------------------9分

(3)由(2)知,k=1时,化为,由得,

点Q到AB的距离为,---------10分

-----------11分

令,则,令得:

,

∴在和(0,上都是增函数,

在是减函数,------------13分

所以无最大值.----------------14分