
设函数 .
.

(1)在区间 上画出函数
上画出函数 的图象
;
的图象
;
(2)设集合 . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明.
之间的关系,并给出证明.
(1)详见解析; (2) .
.
【解析】
试题分析:(1)根据函数的具体特点采用列表描点的基本方法,区间 的端点
的端点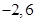 要单独考虑,另外还要考虑到函数
要单独考虑,另外还要考虑到函数 的零点,含有绝对值函数
的零点,含有绝对值函数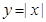 的图象的规律:
的图象的规律: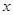 轴上方的不变,
轴上方的不变,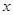 轴下方的翻到
轴下方的翻到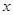 轴上方,这样就可画出函数在区间
轴上方,这样就可画出函数在区间 上的图象; (2)由不等式
上的图象; (2)由不等式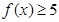 可转化为求出方程
可转化为求出方程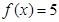 的根,再结合(1)中所作函数的图象,利用函数图象的单调性,即可确定出不等式
的根,再结合(1)中所作函数的图象,利用函数图象的单调性,即可确定出不等式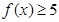 的解集
的解集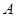 ,借助于数轴可分析
,借助于数轴可分析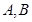 出的关系.
出的关系.
试题解析:(1)函数 在区间
在区间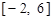 上画出的图象如下图所示:
上画出的图象如下图所示:
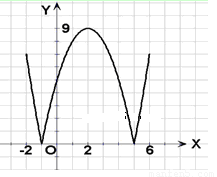 5分
5分
(2)方程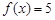 的解分别是
的解分别是 和
和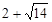 ,由于
,由于 在
在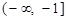 和
和 上单调递减,在
上单调递减,在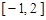 和
和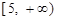 上单调递增,因此
上单调递增,因此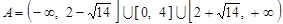 . 8分
. 8分
由于 . 10分
. 10分
考点:1.函数的图象和性质;2.集合的运算


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源:2013-2014学年河南省高三年级12月月考理科数学试卷(解析版) 题型:解答题
设函数 .
.

(1)在区间 上画出函数
上画出函数 的图象
;
的图象
;
(2)设集合 . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明.
之间的关系,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2014届山东省临沂市高三9月月考理科数学试卷(解析版) 题型:解答题
设函数 .
.
(1)在区间 上画出函数
上画出函数 的图象
;
的图象
;
(2)设集合 . 试判断集合
. 试判断集合 和
和 之间
之间
的关系,并给出证明 ;
(3)当 时,求证:在区间
时,求证:在区间 上,
上, 的图象位于函数
的图象位于函数 图象的上方.
图象的上方.

查看答案和解析>>
科目:高中数学 来源:2014届江苏省淮安市高一第一学期期末考试数学试卷 题型:解答题
(本题满分16分)设函数 .
.
(1)在区间 上画出函数
上画出函数 的图象;
的图象;
(2)根据图象写出该函数在 上的单调增区间;
上的单调增区间;
(3)方程 在区间
在区间 有两个不同的实数根,求
有两个不同的实数根,求 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源:2011年辽宁省名校高三数学单元测试:三角函数与三角恒等变换(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com