
有一个倒放着的轴截面为正三角形的圆锥形容器,内盛有高为
h的水,放入一铁球后,上升的水面恰好和球面相切,求球面上的点到圆锥顶点的最小距离.|
解:如图是容器的轴截面△ VGH,它截球O所得的截面为圆O,截水平面得到交线DE.于是△ VDE是正三角形,且圆O是△VDE的内切圆,其中A、C是切点.连结 VC,显然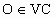 ,OV与圆O相交于B. ,OV与圆O相交于B.
在球面任选一个异于 B的点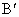 . .
在△  中, 中,
∵ 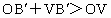 , ,
即 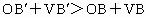 ,且 ,且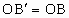 . .
∴ 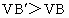 . .
∴ VB的长度是球面上的点到圆锥顶点的最小距离.设球 O的半径为R.在 Rt△VOA中,∵∠OVA=30°,∠OAV=92°,∴ VO=2×OA=2R,∴VC=3R, . .
∴圆锥 VC的体积等于 . .
球 O的体积为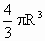 . .
设起始的水平线和圆锥轴截面的交线为 MN.
 , ,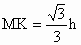 . .
水的体积为 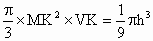 . .
依题意,有 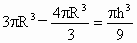 . .
解之,得  , ,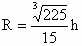 . .
∵ VB=R,∴球面上的点到圆锥顶点的最短距离等于  . .
|


科目:高中数学 来源:数学教研室 题型:044
有一个倒放着的轴截面为正三角形的圆锥形容器,内盛有高为h的水,放入一铁球后,上升的水面恰好和球面相切,求球面上的点到圆锥顶点的最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com