
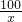 ,其余费用每小时480元,
,其余费用每小时480元,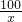 •.3x2+
•.3x2+ =30x+
=30x+
 ≥2
≥2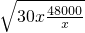 =1200
=1200 ,即x=40时取等
,即x=40时取等

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期第一次月考理科数学试卷 题型:填空题
如下图,为了测量正在海面匀速行驶的某轮船的速度,在海岸上选取距离1千米的两个观察点 ,在某天10:00观察到该轮船在
,在某天10:00观察到该轮船在 处,此时测得
处,此时测得 ,2分钟后该轮船行驶至
,2分钟后该轮船行驶至 处,此时测得
处,此时测得 ,则该轮船的速度为
千米/分钟.
,则该轮船的速度为
千米/分钟.

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com