
求证: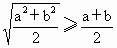
证明:要证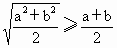 ①
①
只要证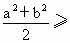 _______________②
_______________②
要证②只要证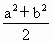 ________________
________________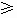 0③
0③
要证③只要证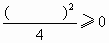 ④,显然④是成立的,当且仅当a=b时,④中的等号成立
④,显然④是成立的,当且仅当a=b时,④中的等号成立
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
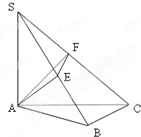 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修1-2) 2009-2010学年 第37期 总第193期 北师大课标 题型:013
求证:![]() -1>
-1>![]() -
-![]() .证明:要证
.证明:要证![]() -1>
-1>![]() -
-![]() ,只需证
,只需证![]() +
+![]() >
>![]() +1,即证7+2
+1,即证7+2![]() +5>11+2
+5>11+2![]() +1,
+1,![]() >
>![]() ,因为35>11,所以原不等式成立.以上证明运用了
,因为35>11,所以原不等式成立.以上证明运用了
分析法
综合法
分析法与综合法综合使用
间接证明
查看答案和解析>>
科目:高中数学 来源: 题型:022
求证:
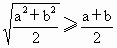
证明:要证
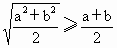 ①
①
只要证
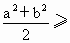 _______________②
_______________②
要证
②只要证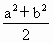 ________________
________________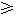 0③
0③
要证
③只要证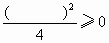 ④,显然④是成立的,当且仅当a=b时,④中的等号成立
④,显然④是成立的,当且仅当a=b时,④中的等号成立查看答案和解析>>
科目:高中数学 来源: 题型:

证明:要证AF⊥SC,只需证SC⊥平面AEF,只需证AE⊥SC(因为___________),只需证___________,只需证AE⊥BC(因为___________),只需证BC⊥平面SAB,只需证BC⊥SA(因为___________).由SA⊥平面ABC可知,上式成立.所以,AF⊥SC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com