用总长44.8m的钢条制做一个底面是等腰三角形的直三棱柱容器的框架,如果所制做容器的底面的腰长比底边长的一半长1m,那么底面的底边,腰及容器的高为多少时容器的容积最大?(参考数据2.662=7.0756,3.342=11.1556)
【答案】
分析:设出底面边长为2x,用x表示出三棱柱的底面的腰长,三棱柱的高,从而得到三棱柱的体积与x的函数关系是解决本题的关键,可以利用导数为工具确定出最大容积时候的x的值,实现该问题的解答.
解答:解:设容器底面等腰三角形的底边长为2xm,则腰长为(x+1)m,
高为
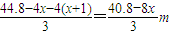
,
设容器的容积为Vm
3,底面等腰三角形底边上的高为
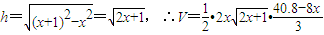
=
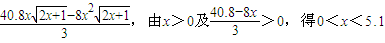
,

,
令V′=0,得x
2-2.66x-1.02=0,(x-3)(x+0.34)=0,由x>0,解得x=3
当0<x<3时V′>0;3<x<5.1时,V′<0,因此,当x=3时,V有最大值.
答:容器的底面等腰三角形的底边长为6m,腰长为4m,容器的高为5.6m时容器的体积最大.
点评:本题考查函数的模型思想和意识,考查设未知数表示函数关系的思想,注意实际问题函数的定义域,依据给出的函数表达式利用导数为工具确定所给函数的最值,考查学生的导数工具意识.

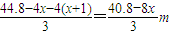 ,
,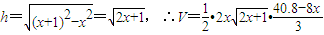
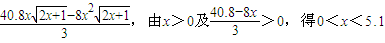 ,
, ,
,

 寒假学与练系列答案
寒假学与练系列答案