Question

选修4-5：不等式证明选讲
已知实数a，b，c，d满足a+b+c+d=3，a²+2b²+3c²+6d²=5，求a的取值范围．

Answer 1

解：由柯西不等式得
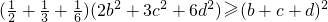
即2b²+3c²+6d²≥（b+c+d）²…（4分）
将条件代入可得5-a²≥（3-a）²，解得1≤a≤2…（6分）
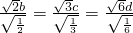
当且仅当时等号成立，
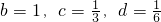
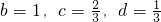
可知时a_max=2，时，a_min=1，
所以a的取值范围是[1，2]．…（10分）
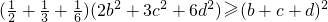
分析：由柯西不等式得，即2b²+3c²+6d²≥（b+c+d）²，将条件代入，我们就可以求出a的取值范围．
点评：柯西不等式的特点：一边是平方和的积，而另一边为积的和的平方，因此，当欲证不等式的一边视为“积和结构”或“平方和结构”，再结合不等式另一边的结构特点去尝试构造．