解:(Ⅰ)∵抛物线
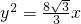
的焦点为
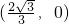
,(1分)
∴设中心在原点,右焦点为
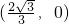
的双曲线C的方程为

.
∵
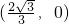
到双曲线的一条准线的距离为

,
∴
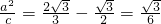
.(2分)
∴
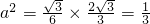
.∴

.(3分)
∴双曲线C的方程为3x
2-y
2=1.(4分)
(Ⅱ)(1)由

得(3-k
2)x
2-2kx-2=0.(5分)
由

得
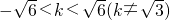
.①(7分)
设A(x
1,y
1),B(x
2,y
2).
∵OA⊥OB,∴y
2y
1+x
2x
1=0,y
1=kx
1+1,y
2=kx
2+1.(9分)
∴(kx
1+1)(kx
2+1)+x
1x
2=0.即x
1x
2(1+k
2)+k(x
1+x
2)+1=0.②
将
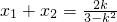
,
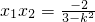
,代入②,解得k=±1,满足①.
∴k=±1时,以AB为直径的圆过原点.(10分)
(2)假设存在实数k,使A、B关于直线y=ax对称(a为常数),
则
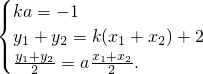
由④、⑤得a(x
1+x
2)=k(x
1+x
2)+2.(12分)
将
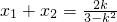
代入上式,得2ak=6,∴ak=3.与③矛盾.(13分)
∴不存在实数k,使A、B关于直线y=ax对称.(14分)
分析:(I)求出抛物线的焦点坐标,求出双曲线的准线方程,利用双曲线中a,b,c的关系求出双曲线方程.
(II)(1)将直线与双曲线方程联立,利用韦达定理得到两交点坐标满足的条件;注意判别式大于0求出斜率的范围;
将以AB为直径的圆过原点转化为OA⊥OB即

,将韦达定理代入向量等式求出k.
(2)利用两点关于直线对称满足两点的中点在直线上;两点连线与对称轴垂直列出方程组,将韦达定理代入得到a,k关系.判断出是否存在.
点评:本题考查双曲线中参数a,b,c的关系、考查解决直线与圆锥曲线的位置关系常将它们的方程联立,利用韦达定理处理、
处理两点关于直线对称的问题常借用两点的中点在对称轴上;两点连线与对称轴垂直.

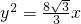 的焦点,且该点到双曲线的一条准线的距离为
的焦点,且该点到双曲线的一条准线的距离为 .
.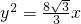 的焦点为
的焦点为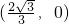 ,(1分)
,(1分)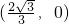 的双曲线C的方程为
的双曲线C的方程为 .
.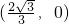 到双曲线的一条准线的距离为
到双曲线的一条准线的距离为 ,
,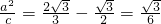 .(2分)
.(2分)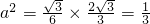 .∴
.∴ .(3分)
.(3分) 得(3-k2)x2-2kx-2=0.(5分)
得(3-k2)x2-2kx-2=0.(5分) 得
得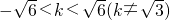 .①(7分)
.①(7分)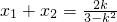 ,
,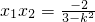 ,代入②,解得k=±1,满足①.
,代入②,解得k=±1,满足①.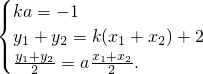 由④、⑤得a(x1+x2)=k(x1+x2)+2.(12分)
由④、⑤得a(x1+x2)=k(x1+x2)+2.(12分)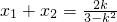 代入上式,得2ak=6,∴ak=3.与③矛盾.(13分)
代入上式,得2ak=6,∴ak=3.与③矛盾.(13分) ,将韦达定理代入向量等式求出k.
,将韦达定理代入向量等式求出k.

 的焦点,且该点到双曲线的一条准线的距离为
的焦点,且该点到双曲线的一条准线的距离为 .
.