Question

为了了解某地区高三学生的身体发育情况，抽查了地区内100名年龄为17.5～18岁的男生的体重情况，结果如下(单位：kg).

56.5     69.5     65     61.5     64.5     66.5     64     64.5     76     58.5 72      73.5      56     67      70       57.5     65.5   68       71     75 62      68.5      62.5    66      59.5      63.5     64.5   67.5     73     68 55      72        66.5   74       63       60      55.5    70      64.5    58 64      70.5      57     62.5      65       69      71.5    73      62     58 76      71        66     63.5     56       59.5     63.5    65      70     74.5 68.5    64        55.5    72.5     66.5      68      76      57.5    60     71.5 57     69.5       74     64.5      59       61.5     67      68     63.5    58 59     65.5       62.5    69.5      72      64.5     75.5     68.5    64     62 65.5   58.5       67.5    70.5       65       66      66.5     70     63     59.5

试根据上述数据画出样本的频率分布直方图.

Answer 1

思路分析：本题考查样本频率分布表及样本频率分布直方图的作法.样本数据小于某一数值的频率叫做该数值点的累积频率.利用样本的累积频率，可以对总体的分布进行估计，这是由于：对任意常数a，P(总体取值＜a)≈样本数据小于a的频率≈累积频率折线上横坐标为a的点的纵坐标(特别地，a是一个分组点时第二个“≈”即为等号)，而且对任意常数a₁＜a₂，P(a₁≤总体取值＜a₂)≈累积频率折线图上横坐标各为a₁,a₂的两点的纵坐标之差，即a₂点的累积频率-a₁点的累积频率.

解：按照下列步骤获得样本的频率分布：

(1)求最大值与最小值的差.

在上述数据中，最大值是76，最小值是55，极差是76-55=21.

(2)确定组距与组数.

如果将组距定为2，那么由21÷2=10.5，组数为11，这个组数适合.于是组距为2，组数为11.

(3)决定分点.

    根据本例中数据的特点，第1小组的起点可取为54.5，第1小组的终点可取为56.5，为了避免一个数据既是起点，又是终点从而造成重复计算，我们规定分组的区间是“左闭右开”的.这样，所得到的分组是

［54.5，56.5)，［56.5，58.5)，…，［74.5，76.5).

(4)列频率分布表.

分组	频数累计	频数	频率
［54.5，56.5)	2	2	0.02
［56.5，58.5)	8	6	0.06
［58.5，60.5)	18	10	0.10
［60.5，62.5)	28	10	0.10
［62.5，64.5)	42	14	0.14
［64.5，66.5)	58	16	0.16
［66.5，68.5)	71	13	0.13
［68.5，70.5)	82	11	0.11
［70.5，72.5)	90	8	0.08
［72.5，74.5)	97	7	0.07
［74.5，76.5)	100	3	0.03
合计	100	100	1.00

(5)绘制频率分布直方图.

频率分布直方图如图2-2-3所示.

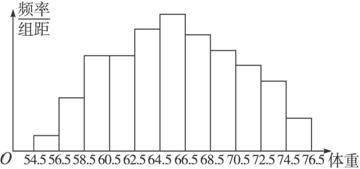
                                   图2-2-3

    方法归纳 由于图中各小长方形的面积等于相应各组的频率，这个图形的面积的形式反映了数据落在各个小组的频率的大小.在反映样本的频率分布方面，频率分布表比较确切，频率分布直方图比较直观，它们起着相互补充的作用.在得到了样本的频率后，就可以对相应的总体情况作出估计.

    例如可以估计，体重在[64.5，66.5)kg的学生最多，约占学生总数的16%；体重小于58.5 kg的学生较少，约占8%等等.

    与频率分布表相比较，频率直方图能直观表明数据的分布形状，但原始数据不能在图中表示，说明直方图丢失了一些信息.