

科目:高中数学 来源:不详 题型:解答题
 设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间 ,求你离家前不能看到报纸(称事件A)的概率是多少?
设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间 ,求你离家前不能看到报纸(称事件A)的概率是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 2名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
2名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多. 列联表;
列联表;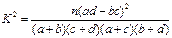 ,
,
 ,可能用到数据:
,可能用到数据: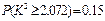 ,
,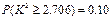 ,
,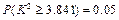 ,
,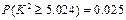 .)
.)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 设该超市在某个时段内购物的人数为36人,其中有12位顾客自己带了购物袋,现从这36人中随机抽取2人.
设该超市在某个时段内购物的人数为36人,其中有12位顾客自己带了购物袋,现从这36人中随机抽取2人. ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分)
分) 个面上分别标有数字
个面上分别标有数字 ).将桌面上骰子全部抛掷在桌面上,然后拿掉那些朝上点数为奇数的骰子,如果桌面上没有了骰子,停止抛掷,如果桌面上还有骰子,继续抛掷桌面上的剩余骰子. 记抛掷两次之内(含两次)去掉的骰子的颗数为
).将桌面上骰子全部抛掷在桌面上,然后拿掉那些朝上点数为奇数的骰子,如果桌面上没有了骰子,停止抛掷,如果桌面上还有骰子,继续抛掷桌面上的剩余骰子. 记抛掷两次之内(含两次)去掉的骰子的颗数为 .
. ;
;  的分布列及期望
的分布列及期望  .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 .现投掷这三枚硬币各1次,设
.现投掷这三枚硬币各1次,设 为得到的正面个数,则随机变量
为得到的正面个数,则随机变量 的数学期望
的数学期望 =" " ▲ .
=" " ▲ .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 和
和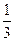 ,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为
,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为 ,至少答对一题即可被聘用(假设每个环节的每个题目回答正确与否是相互独立的)
,至少答对一题即可被聘用(假设每个环节的每个题目回答正确与否是相互独立的) ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com