
已知集合 ,
,


 .若存在实数
.若存在实数 使得
使得 成立,称点
成立,称点 为“£”点,则“£”点在平面区域
为“£”点,则“£”点在平面区域 内的个数是 (
)
内的个数是 (
)
A. 0 B. 1 C. 2 D. 无数个
科目:高中数学 来源:2013-2014学年湖北省等八校高三第一次联考文科数学试卷(解析版) 题型:选择题
已知集合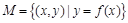 ,若对于任意
,若对于任意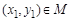 ,存在
,存在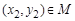 ,使得
,使得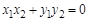 成立,
则称集合
成立,
则称集合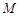 是“理想集合”, 则下列集合是“理想集合”的是( )
是“理想集合”, 则下列集合是“理想集合”的是( )
A.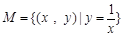 B.
B.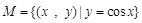
C.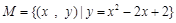 D.
D.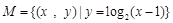
查看答案和解析>>
科目:高中数学 来源:2013年上海市四区(静安、杨浦、青浦、宝山)高考二模理科数学试卷(解析版) 题型:选择题
已知集合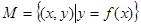 ,若对于任意
,若对于任意 ,存在
,存在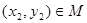 , 使得
, 使得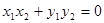 成立,则称集合
成立,则称集合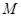 是“
是“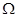 集合”. 给出下列4个集合:
集合”. 给出下列4个集合:
① 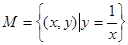 ②
②

③  ④
④

其中所有“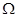 集合”的序号是
( )
集合”的序号是
( )
A.②③ . B.③④ . C.①②④. D.①③④.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省、二中高三上学期期末联考理科数学卷(解析版) 题型:选择题
已知集合 ,
,


 。若存在实数
。若存在实数 使得
使得 成立,称点
成立,称点 为“£”点,则“£”点在平面区域
为“£”点,则“£”点在平面区域 内的个数是
内的个数是
A.0 B.1 C.2 D.无数个
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三11月练习数学试卷 题型:解答题
已知集合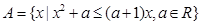 .
.
⑴是否存在实数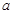 ,使得集合
,使得集合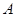 中所有整数的元素和为28?若存在,求出
中所有整数的元素和为28?若存在,求出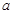 ,若不存在,请说明理由;
,若不存在,请说明理由;
⑵以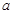 为首项,
为首项,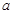 为公比的等比数列前
为公比的等比数列前 项和记为
项和记为 ,对任意
,对任意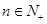 ,均有
,均有 ,求
,求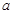 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届北京市高一第一学期期末考试数学 题型:解答题
(本小题满分14分)
已知集合 ,若集合
,若集合 ,且对任意的
,且对任意的 ,存在
,存在 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.
(Ⅰ)分别判断下列集合 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
①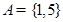 ,
, ;
;
② ,
, .
.
(Ⅱ)若集合 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: ;
;
(Ⅲ)若集合 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com