
分析 (1)根据$(\frac{5π}{6}+α)+(\frac{π}{6}-α)=π$,构造同角化简即可.
(2)根据$\frac{2π}{3}-α=\frac{π}{2}+(\frac{π}{6}-α)$,构造同角化简即可.
解答 解:由题意$cos(\frac{π}{6}-α)=\frac{{\sqrt{3}}}{3}$.
(1)∵$(\frac{5π}{6}+α)+(\frac{π}{6}-α)=π$,
∴$cos(\frac{5π}{6}+α)=cos[π-(\frac{π}{6}-α)]=-cos(\frac{π}{6}-α)=-\frac{{\sqrt{3}}}{3}$.
(2)∵$\frac{2π}{3}-α=\frac{π}{2}+(\frac{π}{6}-α)$,
∴$sin(\frac{2π}{3}-α)=sin[\frac{π}{2}+(\frac{π}{6}-α)]=cos(\frac{π}{6}-α)=\frac{{\sqrt{3}}}{3}$.
点评 本题考查了诱导公式的运用,角度的构造思想.属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
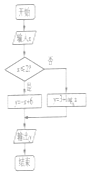
| A. | (1,2] | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
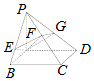 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F
如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
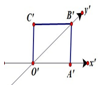 如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$.
如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).
如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com