
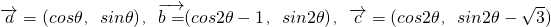 .其中θ≠kπ,k∈Z.
.其中θ≠kπ,k∈Z. ;
;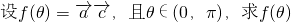 的值域.
的值域.
 ⊥
⊥


 ,
, 与
与 的数量,再通过三角函数公式化简得这个数量积等于零,从而得到向量
的数量,再通过三角函数公式化简得这个数量积等于零,从而得到向量 与向量
与向量 互相垂直;
互相垂直; ,再通过二倍角的三角函数公式进行化简,得到
,再通过二倍角的三角函数公式进行化简,得到 ,最后根据θ∈(0,π),可以得出函数f(θ)的值域.
,最后根据θ∈(0,π),可以得出函数f(θ)的值域.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| x |
| y |
| x |
| y |
| x |
| y |
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高一下学期摸底考试数学试卷 题型:选择题
已知向量 ,其中O是坐标原点,若A,B,C三点共线,则实数k=( )
,其中O是坐标原点,若A,B,C三点共线,则实数k=( )
A. B.
B. C.11
D.
C.11
D. 或11
或11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com