
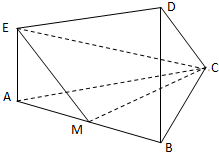
 (2012•临沂一模)在如图所示的几何体中,四边形ABDE为梯形,AE∥BD,AE⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M为AB的中点;
(2012•临沂一模)在如图所示的几何体中,四边形ABDE为梯形,AE∥BD,AE⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M为AB的中点;
| 2 |
| 3 |
| 2 |
| 5 |
| EM×MC |
| EC |
| ||
| 5 |
| a | ||||
|
| ||
| 6 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012•临沂一模)为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了200位老年人,结构如下:
附:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x+1 |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com