科目：高中数学 来源：2017届河南南阳一中高三理上学期月考四数学试卷（解析版） 题型：填空题
《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共为3升，下面3节的容积共4升，则第5节的容积为 升．
查看答案和解析>>
科目：高中数学 来源：2017届贵州遵义南白中学高三文上学期联考四数学试卷（解析版） 题型：解答题
已知在四棱锥
中，底面
是矩形，且
，
，
平面
，
、
分别是线段
、
的中点．
（1）证明：
；
（2）若
，求点
到平面
的距离．
查看答案和解析>>
科目：高中数学 来源：2017届贵州遵义南白中学高三文上学期联考四数学试卷（解析版） 题型：选择题
设
，
分别是定义在
上的奇函数和偶函数，当
时，
，且
，则不等式
的解集是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2017届贵州遵义南白中学高三理上学期联考四数学试卷（解析版） 题型：解答题
甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：甲：82 81 79 78 95 88 93 84 乙：92 95 80 75 83 80 90 85
（1）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适？请说明理由；
（2）若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为
，求
的分布列及数学期望
．
查看答案和解析>>
科目：高中数学 来源：2017届江西吉安一中高三理周考三数学试卷（解析版） 题型：解答题
选修4-4：坐标系与参数方程
在平面直角坐标系
中，以坐标原点为极点，
轴正半轴为极轴建立极坐标系，曲线
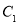的极坐标方程为
．
（1）求
的直角坐标方程；
（2）曲线
的参数方程为
（
为参数），求
与
的公共点的极坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，若复数
，
在复平面内的对应点关于虚轴对称，则
（ ）
B．
C．
D．
在
上是增函数，则实数
的取值范围是（ ）
B．
D．
，当
时，
的概率为（ ）
B．
D．
是三角形的最小内角，则函数
的最小值是（ ）
B．
C．
D．