
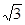 ,第三边上的中线长为2,则三角形的外接圆半径为
,第三边上的中线长为2,则三角形的外接圆半径为 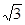 ,AD=2,D为BC边的中点,BC=2x,则BD=DC=x,由cos∠ADB=
,AD=2,D为BC边的中点,BC=2x,则BD=DC=x,由cos∠ADB=  ,cos∠ADC=
,cos∠ADC=  且cos∠ADB=-cos∠ADC,代入可求BC,则可得A=90°,外接圆的直径2R=BC,从而可求
且cos∠ADB=-cos∠ADC,代入可求BC,则可得A=90°,外接圆的直径2R=BC,从而可求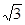 ,AD=2,D为BC边的中点,BC=2x,则BD=DC=x
,AD=2,D为BC边的中点,BC=2x,则BD=DC=x ,
,
 =-
=-



 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com