
 •BE2
•BE2 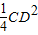 (AB2+AE2)=
(AB2+AE2)= (AC2+AD2)(AB2+AE2),再化简即得结论.
(AC2+AD2)(AB2+AE2),再化简即得结论.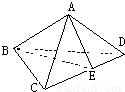
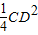 •BE2 =
•BE2 =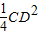 (AB2+AE2)
(AB2+AE2) (AC2+AD2)(AB2+AE2)
(AC2+AD2)(AB2+AE2) (AC2AB2 +AD2AB2 +AC2AE2+AD2AE2 )
(AC2AB2 +AD2AB2 +AC2AE2+AD2AE2 ) (AC2AB2 +AD2AB2+CD2AE2 )
(AC2AB2 +AD2AB2+CD2AE2 )

科目:高中数学 来源:2010-2011学年山东省兖州市高二下学期期末考试数学(文) 题型:解答题
(本小题12分)类比平面直角三角形的勾股定理,试给出空间中四面体性质的猜想,并证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com