
【题目】已知圆C:x2+y2+Dx+Ey+3=0,圆C关于直线x+y﹣1=0对称,圆心在第二象限,半径为![]() .
.
(1)求圆C的方程;
(2)已知不过原点的直线l与圆C相切,且与x轴、y轴上的截距相等,求直线l的方程.
【答案】解:(1)圆C:x2+y2+Dx+3=0的坐标C(﹣![]() ,-
,-![]() ),
),
∵圆C关于直线x+y﹣1=0对称,
∴C(﹣![]() ,-
,-![]() )在直线x+y﹣1=0上,
)在直线x+y﹣1=0上,
即﹣![]() -
-![]() ﹣1=0,即D+E+2=0,
﹣1=0,即D+E+2=0,
半径R=![]() =
=![]() ,
,
即D2+E2=20,
解得![]() 或
或![]() ,此时圆心为(﹣2,1),或(1,﹣2),
,此时圆心为(﹣2,1),或(1,﹣2),
∵圆心在第二象限,∴圆心坐标为(﹣2,1),
则圆C的方程为(x+2)2+(y﹣1)2=2.
(2)设不经过直线截距相等的直线方程为x+y=a,即x+y﹣a=0,
则圆心到直线的距离d=![]() =
=![]() ,
,
即|a+1|=2,解得a=1或a=﹣3,
故直线方程为x+y﹣1=0或x+y+3=0.
【解析】(1)求出圆心坐标,根据圆心在直线上以及圆的半径建立方程关系即可求圆C的方程;
(2)设直线的截距式方程为x+y=a,利用直线和圆相切建立方程关系即可.


科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函数g(x)=|logax﹣1|的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若b= ![]() ,c=1,求△ABC的面积.
,c=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F1、F2是一对相关曲线的焦点,P是它们在第一象限的交点,当∠F1PF2=60°时,这一对相关曲线中双曲线的离心率是( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017年第二次全国大联考江苏卷】若无穷数列![]() 满足:
满足:![]() 恒等于常数
恒等于常数![]() ,则称
,则称![]() 具有局部等差数列
具有局部等差数列![]() .
.
(1)若![]() 具有局部等差数列
具有局部等差数列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有局部等差数列
是否具有局部等差数列![]() ,并说明理由;
,并说明理由;
(3)设![]() 既具有局部等差数列
既具有局部等差数列![]() ,又具有局部等差数列
,又具有局部等差数列![]() ,求证:
,求证:![]() 具有局部等差数列
具有局部等差数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆C过点(1,0),且于直线x=﹣1相切.
(1)求圆心C的轨迹M的方程;
(2)A,B是M上的动点,O是坐标原点,且![]()
![]()
![]() , 求证:直线AB过定点,并求出该点坐标.
, 求证:直线AB过定点,并求出该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
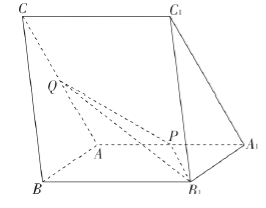
【题目】【2017福建4月质检】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com