练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知A＝{x|x＋1≥0}，B＝{x|x2－2＞0}，全集I＝R，则A∩B为

    [　　]

    A．{x|x≥或x≤－}

    B．{x|x≥－1或x≤}

    C．{x|－1≤x≤}

    D．{x|－≤x≤－1}

    答案：C
    解析：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：013

    已知A＝{x|x≤1}，B＝{x|x＞a}，A∩B≠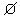，则a的取值是

    [　　]

    A．a＜1
    B．a＞1
    C．a≥1
    D．a≤2

    查看答案和解析>>

    科目：高中数学 来源：2008届海南省农垦中学高三数学第一次月考、数学试题 题型：013

    已知A＝{x||2x－1|≤3，x∈Z}，B＝{x|ax＝1}，若A∪B＝A，则实数a的取值集合为

    [　　]

    A．{－1，0，，1}

    B．{－1，0，1}

    C．{－1，，1}

    D．{1，，0}

    查看答案和解析>>

    科目：高中数学 来源：2014届广东省高一期中考试文科数学试卷A卷（解析版） 题型：解答题

    已知函数f(x)(x∈R)满足f(x)＝，a≠0，f(1)＝1，且使f(x)＝2x成立的实数x只有一个．

    (1)求函数f(x)的表达式；

    (2)若数列{an}满足a1＝，an+1＝f(an)，bn＝－1，n∈N*，证明数列{bn}是等比数列，并求出{bn}的通项公式；

    (3)在(2)的条件下，证明：a1b1＋a2b2＋…＋anbn<1(n∈N*)．

    【解析】解： (1)由f(x)＝，f(1)＝1，得a＝2b＋1.

    由f(x)＝2x只有一解，即＝2x，

    也就是2ax2－2(1＋b)x＝0(a≠0)只有一解，

    ∴b＝－1.∴a＝－1.故f(x)＝.…………………………………………4分

    (2)an＋1＝f(an)＝(n∈N*)，bn＝－1， ∴＝＝＝，

    ∴{bn}为等比数列，q＝.又∵a1＝，∴b1＝－1＝，

    bn＝b1qn－1＝n－1＝n(n∈N*)．……………………………9分

    (3)证明：∵anbn＝an＝1－an＝1－＝，

    ∴a1b1＋a2b2＋…＋anbn＝＋＋…＋<＋＋…＋

    ＝＝1－<1(n∈N*)．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A＝{x||x-2|≥1},B={x|x4-x＞1},C={x|2x2-9x+a＜0}.

    （1）求（A）∩B;

    （2）若C［（A）∩B］,求a的范围.

    查看答案和解析>>

    同步练习册答案