
已知复数满足z+|z|=2+8i,求复数z.
|
解法一:设z=a+bi(a、b∈R),则|z|= ∴a+ ∴z=-15+8i. 解法二:原式可化为z=2-|z|+8i. ∵|z|∈R,∴2-|z|是z的实部. 于是|z|= 即|z|2=68-4|z|+|z|2, ∴|z|=17,代入z=2-|z|+8i,得z=-15+8i. 思路分析:常规解法:设z=a+bi(a、b∈R),代入等式后,可利用复数相等的充要条件,求出a、b,也可以巧妙利用|z|∈R,移项后得到复数的实部,再取模可得关于|z|的方程,求解即可. |
|
z为复数,但|z|为实数,复数相等的定义即实部与实部相等,虚部与虚部相等.需明确谁是实部,谁是虚部,同时,把复数z看作整体的方法值得借鉴. |


科目:高中数学 来源:2012-2013学年浙江省温州中学高三(上)10月月考数学试卷(理科)(解析版) 题型:选择题
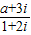 满足z•i=2-i,i为虚数单位,则z的虚部是( )
满足z•i=2-i,i为虚数单位,则z的虚部是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com