
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
 (2012•福州模拟)对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=
(2012•福州模拟)对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三3月质量检查试题文科数学试卷 题型:填空题
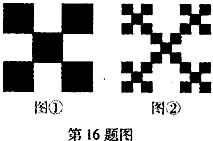
对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=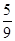 ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积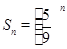 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=____________
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=____________
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省厦门一中集美分校高三(上)期末数学模拟试卷(文科)(解析版) 题型:填空题
 ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积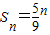 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .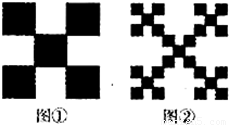
查看答案和解析>>
科目:高中数学 来源:2012年福建省福州市高三3月质量检查数学试卷(文科)(解析版) 题型:填空题
 ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积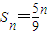 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .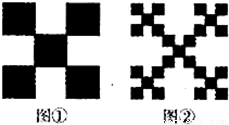
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com