
(2007高考广东)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
|
x |
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤;试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
【解析】
(1)散点图如右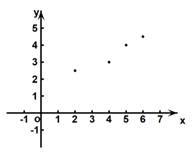 ;……4分
;……4分
(2)方法一:设线性回归方程为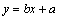 ,则
,则
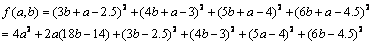
∴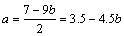 时,
时, 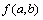 取得最小值
取得最小值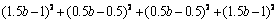 ,
,
即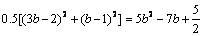 ,∴
,∴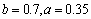 时
时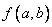 取得最小值.
取得最小值.
所以线性回归方程为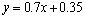 .……10分
.……10分
方法二:由系数公式可知,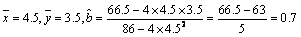
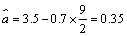 ,所以线性回归方程为
,所以线性回归方程为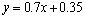 .
.
(3)x=100时,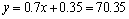 ,所以预测生产100吨甲产品的生产能耗比技术改造前降低
,所以预测生产100吨甲产品的生产能耗比技术改造前降低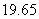 吨标准煤.……14分
吨标准煤.……14分
【点评】本题考查回归分析的基本思想,是课标区三年来考查的唯一的一道解答题。求线性回归方程的方法一这实际上是重复了回归系数公式的推导过程,这里的另一个解决方法是对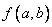 我们再按
我们再按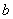 集项,
集项,
即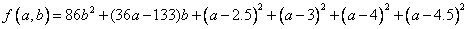 ,而这个时候,当
,而这个时候,当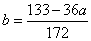 时
时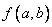 有最小值,结合上面解法中
有最小值,结合上面解法中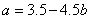 时
时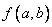 有最小值,组成方程组就可以解出
有最小值,组成方程组就可以解出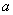 ,
,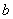 的值;方法二前提是正确地使用回归系数的计算公式,一般考试中都会给出这个公式,但要注意各个量的计算;最后求出的
的值;方法二前提是正确地使用回归系数的计算公式,一般考试中都会给出这个公式,但要注意各个量的计算;最后求出的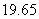 是指的平均值或者是估计值,不是完全确定的值.对于本题我们可以计算题目所给的数据组的相关系数
是指的平均值或者是估计值,不是完全确定的值.对于本题我们可以计算题目所给的数据组的相关系数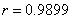 ,相关指数
,相关指数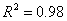 .这说明
.这说明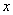 ,
,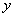 具有很强的线性相关性,说明解释变量对预报变量的贡献率是
具有很强的线性相关性,说明解释变量对预报变量的贡献率是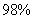 ,即耗煤量的
,即耗煤量的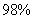 是来自生产量,只有约
是来自生产量,只有约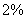 来自其它因素,这与我们的直观感觉是十分符合的.
来自其它因素,这与我们的直观感觉是十分符合的.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
(07年广东卷文)图l是某县参加2007年高考的学生身高条形统计图,

从左到右的各条形表示的学生人数依次记为![]() 、
、![]() 、…、
、…、![]() (如
(如![]() 表示身高(单位:
表示身高(单位:![]() )在
)在
[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180![]() (含160
(含160![]() ,不含180
,不含180![]() )的学生人数,那么在流程图中的判断框内应填写的条件是
)的学生人数,那么在流程图中的判断框内应填写的条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com