Question

21．已知方向向量为v=(1,)的直线l过点（0，－2）和椭圆C：(a>b>0)的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.

（Ⅰ）求椭圆C的方程；

（Ⅱ）是否存在过点E（－2，0）的直线m交椭圆C于点M、N，满足cot∠MON≠0（O为原点）.若存在，求直线m的方程；若不存在，请说明理由.

Answer 1

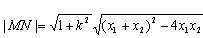
21.（I）解法一：直线，  ①

过原点垂直的直线方程为，  ②

解①②得

∵椭圆中心O（0，0）关于直线的对称点在椭圆C的右准线上，

∵直线过椭圆焦点，∴该焦点坐标为（2，0）.

  故椭圆C的方程为  ③

解法二：直线.

设原点关于直线对称点为（p，q），则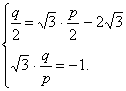

解得p=3.

∵椭圆中心O（0，0）关于直线的对称点在椭圆C的右准线上，

    ∵直线过椭圆焦点，∴该焦点坐标为（2，0）.

  故椭圆C的方程为  ③

（II）解法一：设M（），N（）.

当直线m不垂直轴时，直线代入③，整理得

 

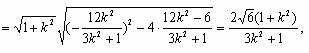
点O到直线MN的距离

      

即

      

       即

       整理得

       当直线m垂直x轴时，也满足.

       故直线m的方程为

       或或

       经检验上述直线均满足.

所以所求直线方程为或或

解法二：设M（），N（）.

       当直线m不垂直轴时，直线m：y=k(x+2)代入③，整理得

        

       ∵E（－2，0）是椭圆C的左焦点，

       ∴|MN|=|ME|+|NE|=

    以下与解法一相同.

解法三：设M（），N（）.

       设直线，代入③，整理得

     

       |y₁-y₂|==

      

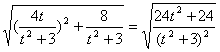
即

      

      

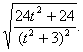
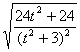       ∴=，整理得      

       解得或

       故直线m的方程为或或

       经检验上述直线方程为

       所以所求直线方程为或或