
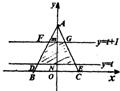
 如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.
如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象. | 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
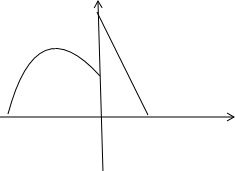
 如图,在坐标平面内作两条与实轴平行的直线l1:y=3,l2:y=-1,
如图,在坐标平面内作两条与实轴平行的直线l1:y=3,l2:y=-1,| x2 |
| 25 |
| y2 |
| 16 |
查看答案和解析>>
科目:高中数学 来源:上海市十三校2012届高三第二次联考数学文科试题 题型:044
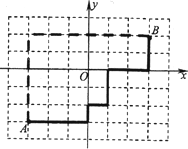
现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1),B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
(1)已知A(-3,-3),B(3,2),求A、B两点的距离D(AB).
(2)求到定点M(1,2)的“直角距离”为2的点的轨迹方程.
并写出所有满足条件的“格点”的坐标(格点是指横、纵坐标均为整数的点).
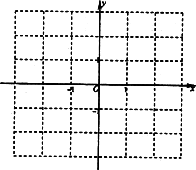
(3)求到两定点F1、F2的“直角距离”和为定值2a(a>0)的动点轨迹方程,并在直角坐标系内作出该动点的轨迹.
①F1(-1,0),F2(1,0),a=2;
②F1(-1,-1),F2(1,1),a=2;
③F1(-1,-1),F2(1,1),a=4.
查看答案和解析>>
科目:高中数学 来源:上海市十三校2012届高三第二次联考数学理科试题 题型:044
现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1),B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.

(1)在平面直角坐标系中,写出所有满足到原点的“直角距离”为2的“格点”的坐标.(格点指横、纵坐标均为整数的点)
(2)求到两定点F1、F2的“直角距离”和为定值2a(a>0)的动点轨迹方程,并在直角坐标系内作出该动点的轨迹.
①F1(-1,0),F2(1,0),a=2;
②F1(-1,-1),F2(1,1),a=2;
③F1(-1,-1),F2(1,1),a=4.
(3)写出同时满足以下两个条件的“格点”的坐标,并说明理由(格点指横、纵坐标均为整数的点).
①到A(-1,-1),B(1,1)两点“直角距离”相等;
②到C(-2,-2),D(2,2)两点“直角距离”和最小.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
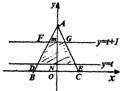 如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.
如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com