
分析 (1)切点在曲线上,求得b=-2,对函数求导,利用导数的几何意义,得出f'(0)=-2,从而求得a=2;
(2)曲线y=f(x)上存在三条斜率为k的切线,等价于其导数等于k有三个解,结合函数图象的走向,从而确定出其范围应该介于极小值和极大值之间即可.
解答 解:(1)f(x)=(x2-2ax+2)ex,
f(0)=2e0=2,2+b=0,得b=-2,
f′(x)=(x2-2ax+2+2x-2a)ex=[x2+(2-2a)x+2-2a]ex,
f′(0)=2-2a=-2,求得a=2,
∴a=2,b=-2.
(2)f′(x)=[x2+(2-2a)x+2-2a]ex,
令h(x)=f(x),依题知存在k使h(x)=k有三个不同的实数根,
h′(x)=(x2-2ax+2+2x-2a+2x-2a+4)ex=[x2+(4-2a)x+4-4a]ex,
令h′(x)=[x2+(4-2a)x+4-4a]ex=0,求得x1=-2,x2=2a-2,
由a>0知x1<x2,
则f′(x)在(-∞,-2),(2a-2,+∞)上单调递增,
在(-2,2a-2)上单调递减.
当x→-∞时,f'(x)→0,当x→+∞时,f'(x)→+∞,
∴f′(x)的极大值为f'(-2)=e-2(2a+2),
f′(x)的极小值为f'(2a-2)=e2a-2(2-2a),
所以此时e2a-2(2-2a)<k<e-2(2a+2).
点评 本题考查导数的运用:求切线的斜率和单调区间、极值,考查函数方程的转化思想,考查运算能力,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
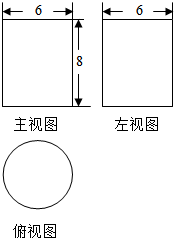 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )| A. | 133π | B. | 100π | C. | 66π | D. | 166π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | x | y |
| 总计 | 60 | z | 110 |
| P(K2≥K) | 0.10 | 0.05 | 0.01 | 0.005 |
| K | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com