练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知p：x2+mx+1=0有两个不等的负根，q：方程4x2+4（m-2）x+1=0（m∈R）无实根，求：使p为真命题且q也为真命题的m的取值范围．
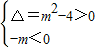
    【答案】分析：利用“3个二次”的关系：p：x2+mx+1=0有两个不等的负根?，即可解出；q：方程4x2+4（m-2）x+1=0（m∈R）无实根?△＜0，即可解出．
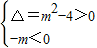
    解答：解：若p为真，则，解得m＞2．
    若q为真，则△=16（m-2）2-16＜0，解得1＜m＜3．
    由p真，q真，即
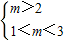
    故m的取值范围是（2，3）．
    点评：熟练掌握“3个二次”的关系是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知p：x2+mx+1=0有两个不等的负根，q：方程4x2+4（m-2）x+1=0（m∈R）无实根，求：使p为真命题且q也为真命题的m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知p:方程x2+mx+1=0有两个不等的负根；q:方程4x2+4(m-2)x+1=0无实根.若p或q为真，p且q为假，求m的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实数根,若p或q为真,p且q为假,求m的取值范围.?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知p:方程x2+mx+1=0有两个不等的负实根;q:方程4x2+4(m-2)x+1=0无实根,若p或q为真,p且q为假,求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4（m－2）x+1＝0无实根.若p或q为真，p且q为假，求m的取值范围.?

    查看答案和解析>>

    同步练习册答案