
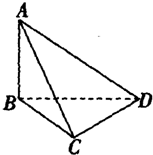
 如图,要测底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,求电视塔AB的高度.
如图,要测底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,求电视塔AB的高度.| 3 |
| AB |
| tan30° |
| 3 |
| 3 |


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
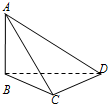
 要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )
要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )A、10
| ||
| B、20m | ||
C、20
| ||
| D、40m |
查看答案和解析>>
科目:高中数学 来源: 题型:
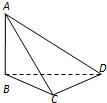 要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为
要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为查看答案和解析>>
科目:高中数学 来源: 题型:
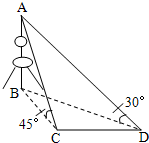 如图所示,要测量底部不能到达的某电视塔AB的高度,在塔的同一侧选择C、D两观测点,且在C、D两点测得塔顶的仰角分别为45°、30°,在水平面上测得∠BCD=120°,C、D两地相距500m,则电视塔AB的高度是( )
如图所示,要测量底部不能到达的某电视塔AB的高度,在塔的同一侧选择C、D两观测点,且在C、D两点测得塔顶的仰角分别为45°、30°,在水平面上测得∠BCD=120°,C、D两地相距500m,则电视塔AB的高度是( )A、100
| ||
| B、400m | ||
C、200
| ||
| D、500m |
查看答案和解析>>
科目:高中数学 来源:三点一测丛书 高中数学 必修5 (江苏版课标本) 江苏版课标本 题型:044
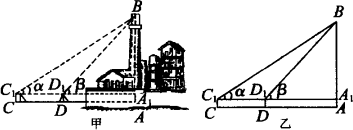
如图甲,要测底部不能到达的烟囱的高AB,从与烟囱底部在同一水平线上的C,D两处,测得烟囱的仰角分别为α=35°![]() 和β=49°
和β=49°![]() ,CD间的距离是11.12米,已知测角仪器高1.52米,求烟囱的高.
,CD间的距离是11.12米,已知测角仪器高1.52米,求烟囱的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com