同时抛掷两枚质地均匀的正方体骰子,它们的每一面分别标有数字,1,2,3,4,5,6计算:
(I)一共有多少种不同的结果;
(II)其中向上的数字之和为7的结果有多少种(列出所有情况);
(III)向上的数字之和为7的概率是多少.
【答案】
分析:(I)每一个一个正方体骰子的结果有6种,因此同时抛掷两枚质地均匀的正方体骰子的结果有36种.
(II)用列举法求得在上面所有结果中其中向上的数字之和为7的有六种.
(III)由于所有36种结果是等可能的,其中向上的数字之和为7的结果(记为事件A)有6种,从而求得向上的数字之和为7的概率.
解答:解:(I)掷一个正方体骰子的结果有6种,把两个正方体骰子分为甲,乙以便区分,
由于甲的每一种结果都可与乙的任一个结果配对,组成同时抛掷两枚质地均匀的正方体骰子的一个结果,
因此同时抛掷两枚质地均匀的正方体骰子的结果有36种.(4分)
(II)在上面所有结果中其中向上的数字之和为7的有(1,6)、(2,5)、(3,4)、(4,3)、(5,2)、(6,1),共有六种.(8分)
(III)由于所有36种结果是等可能的,其中向上的数字之和为7的结果(记为事件A)有6种,
因此
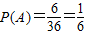
.(11分)
点评:本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于中档题

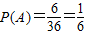 .(11分)
.(11分)
