练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．抛物线y2=8x上横坐标为1的点到其焦点F距离为（　　）
    A．2B．3C．4D．$3\sqrt{2}$

    分析 利用抛物线的定义，转化求解即可．

    解答 解：抛物线y2=8x的焦点坐标（2，0），准线方程为：x=-2，
    抛物线y2=8x上横坐标为1的点到其焦点F距离就是到准线的距离为：3．
    故选：B．

    点评 本题考查抛物线的简单性质的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

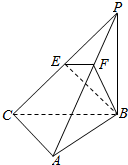    20．如图，三棱锥P-ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=2，E为PC的中点，M为AB的中点，点F在PA上，且2PF=FA．
    （1）求证：BE⊥平面PAC；
    （2）求直线AB与平面BEF所成的角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

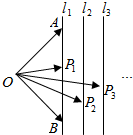    1．如图，已知l1，l2，l3，…ln为平面内相邻两直线距离为1的一组平行线，点O到l1的距离为2，A，B是l1的上的不同两点，点P1，P2，P3，…Pn分别在直线l1，l2，l3，…ln上．若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$（n∈N*），则x1+x2+…+x5+y1+y2+…+y5的值为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

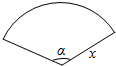    18．如图，用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地，设扇形的半径为xm，面积为Scm2．
    （1）写出S关于x的函数表达式，并求出该函数的定义域；
    （2）当半径x和圆心角α分别是多少时，所围扇形场地的面积S最大，并求S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知直线l经过直线2x+y-5=0与x-2y=0的交点P．
    （Ⅰ）若直线l平行于直线l1：4x-y+1=0，求l的方程；
    （Ⅱ）若直线l垂直于直线l1：4x-y+1=0，求l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知直线l经过直线2x+y-5=0与x-2y=0的交点P，直线l1的方程为4x-y+1=0．
    （Ⅰ）若直线l平行于直线l1，求l的方程；
    （Ⅱ）若直线l垂直于直线l1，求l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．过点A（-1，1）且与直线x+3y+4=0平行的直线l的方程为x+3y-2=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．log25，2-3，${3^{\frac{1}{2}}}$三个数中最小的数是2-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．对于满足|f（n+1）-f（n）|≤（$\frac{1}{10}$）n（n∈N）的所有f（n），若f（0）=1，则f（10）的值所在的区间一定是（　　）
    A．（-1，1）B．（0，2）C．（-$\frac{1}{9}$，$\frac{19}{9}$）D．（-$\frac{1}{5}$，$\frac{9}{5}$）

    查看答案和解析>>

    同步练习册答案