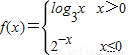练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数，，若f（f（-3））∈[k，k+1），k∈Z，则k=    ，当f（x）=1时，x=    ．
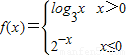    【答案】分析：由已知中分段函数的解析式，，我们将x=-3代入可求出f（-3），再代入f（f（-3）），根据对数的性质，易得到f（f（-3））的范围，进而得到k值，分别讨论两种情况下f（x）=1时，x的值，并根据对应x的取值范围进行检验，即可得到答案．
    解答：解：∵，
    ∴f（f（-3））=f（8）=log38
    又∵log33＜log38＜log39
    ∴1＜log38＜2
    故若f（f（-3））∈[k，k+1），k∈Z，k=1
    若log3x=1，则x=3，满足要求；
    若2-x=1，则x=0，不满足要求；
    故当f（x）=1时，x=3
    故答案为：1，3
    点评：本题考查的知识点是分段函数的函数值，及分段函数给值求值问题，分段函数分段处理，是解答此类问题常用的方法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=-x2+2bx-b
    （1）当b=2时，求函数y=f（x） 在[1，4]上的最值；
    （2）若函数y=f（x） 在[1，4]上仅有一个零点，求b的取值范围；
    （3）是否存在实数b，使得函数y=f（x） 在[1，+∞）上的最大值是2，若存在，求出b的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）是R上的增函数，对实数a，b，若a+b＞0，则有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    x3(x＞0)
    (3-a)x-a(x≤0)
    ，给出下列四个命题：
    （1）当a＞0时，函数f（x）的值域为[0，+∞），
    （2）对于任意的x1，x2∈R，且x1≠x2，若
    f(x1)-f(x2)
    x1-x2
    ＞0恒成立，则a∈[0，3）；  
    （3）对于任意的x1，x2∈（0，+∞），且x1≠x2，恒有
    f(x1)+f(x)2
    2
    ＜f（
    x1+x2
    2
    ）；  
    （4）对于任意的x1，x2∈（0，+∞），且x1≠x2，若不等式|f（x1）-f（x2）|＞t|x1-x2|恒成立，则t的最大值为0．其中正确的有
    （2）（4）
    （2）（4）
    （只填相应的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    解：因为有负根，所以在y轴左侧有交点，因此

    解：因为函数没有零点，所以方程无根，则函数y=x+|x-c|与y=2没有交点，由图可知c>2


     13．证明：（1）令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0

    若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)与已知条件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函数y=f(x)-1的零点

    （2）因为f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函数是奇函数

    数字1，2，3，4恰好排成一排，如果数字i（i=1，2，3，4）恰好出现在第i个位置上则称有一个巧合，求巧合数的分布列。

    查看答案和解析>>

    科目：高中数学 来源：2013届内蒙古巴彦淖尔市中学高二下期中文科数学试卷（解析版） 题型：选择题

     已知函数f(x)=若f(a)+f(1)=0,则实数a的值等于（  ）

    A．-1            B．-3          C．1             D．3

     

    查看答案和解析>>

    同步练习册答案