
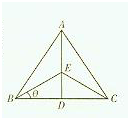
 某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.
某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.| 2-sinθ |
| cosθ |
| π |
| 3 |
| π |
| 6 |
| 2-sinθ |
| cosθ |
| ||
| BE |
| ED |
| BE |
| a |
| 2cosθ |
| asinθ |
| 2cosθ |
| ||
| 2 |
| a |
| 2 |
| 2-sinθ |
| cosθ |
| ||
| 2 |
| π |
| 3 |
| 2-sinθ |
| cosθ |
| π |
| 3 |
| 2sinθ-1 |
| cos2θ |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| 2-sinθ |
| cosθ |
| π |
| 6 |
| 3 |
| 2-sinθ |
| cosθ |
| 3 |
| π |
| 6 |


科目:高中数学 来源: 题型:解答题
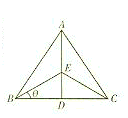 某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.
某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.查看答案和解析>>
科目:高中数学 来源:月考题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com