【题目】下列说法错误的是（ ）
A.在回归分析中，相关指数
越大，说明残差平方和越小，回归效果越好
B.线性回归方程对应的直线
至少经过其样本数据点中的一个点
C.在线性回归分析中，相关系数为
，
越接近于1，相关程度越大
D.在回归直线
中，变量
每增加一个单位，变量
大约增加0.5个单位
开心蛙状元测试卷系列答案科目：高中数学 来源： 题型：
【题目】已知某单位由50名职工，将全体职工随机按1-50编号，并且按编号顺序平均分成10组，先要从中抽取10名职工，各组内抽取的编号依次增加5进行系统抽样.
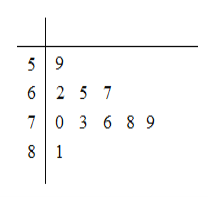
（1）若第五组抽出的号码为22，写出所有被抽出职工的号码；
（2）分别统计这10名职工的体重（单位：公斤），获得体重数据的茎叶图如图所示，求该样本的中位数；
（3）在（2）的条件下，从体重不低于73公斤的职工中随机抽取两名职工，求被抽到的两名职工的体重之和大于或等于154公斤的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点P(1,3)，Q(1,2).设过点P的动直线与抛物线y=x2交于A，B两点，直线AQ，BQ与该抛物线的另一交点分别为C，D.记直线AB，CD的斜率分别为k1，k2.
（1）当
时，求弦AB的长；
（2）当
时，
是否为定值？若是，求出该定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在平面直角坐标系
中，已知椭圆
：
（
），
，
，
，
是椭圆上的四个动点，且
，
，线段
与
交于椭圆内一点
.当点
的坐标为
，且，分别为椭圆的上顶点和右顶点重合时，四边形
的面积为4.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）证明：当点，，，在椭圆上运动时，
（
）是定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知鸡的产蛋量与鸡舍的温度有关，为了确定下一个时段鸡舍的控制温度，某企业需要了解鸡舍的温度
（单位：℃）对某种鸡的时段产蛋量
（单位：
）的影响.为此，该企业收集了7个鸡舍的时段控制温度
和产蛋量
的数据，对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
|
|
|
|
|
|
|
17.4 | 82.3 | 3.6 | 140 | 9.7 | 2935.1 | 35 |
其中
，
.
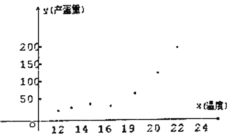
（1）根据散点图判断，
与
哪一个更适宜作为该种鸡的时段产蛋量关于鸡舍时段控制温度的回归方程类型？（给判断即可，不必说明理由）
（2）若用作为回归方程模型，根据表中数据，求出关于的回归方程；
（3）当时段控制温度为28℃时，鸡的时段产蛋量的预报值（精确到0.1）是多少？
附：①对于一组具有线性相关系的数据
，其回归直线
的斜率和截距的最小二乘估计分别为
.
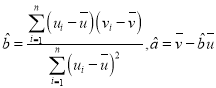②参考值.
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，AB//CD，且
（1）证明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC, 
,且四棱锥P-ABCD的体积为
，求该四棱锥的侧面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从柳州铁一中高二男生中随机选取100名学生，将他们的体重（单位：
）数据绘制成频率分布直方图，如图所示．
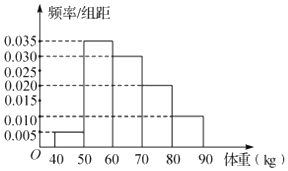
（1）估计该校的100名同学体重的平均值和方差（同一组数据用该组区间的中点值代表）；
（2）若要从体重在
内的两组男生中，用分层抽样的方法选取5人，再从这5人中随机抽取2人，求被抽取的两位同学来自不同组的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
