
分析 (Ⅰ)求出函数的导函数,得到f′(e)=$\frac{1}{e}$,再求出f(e)=lne=1,利用直线方程的点斜式求得曲线y=f(x)在点(e,1)处的切线方程;
(Ⅱ)求出g(x)代入f(x)≥ag(x),分离参数a,构造函数h(x)=$\frac{xlnx}{x-1}$(x≥3),利用导数求其最小值得答案.
解答 解:(Ⅰ)∵f(x)=lnx,
∴f′(x)=$\frac{1}{x}$,则f′(e)=$\frac{1}{e}$.
又f(e)=lne=1,
∴求曲线y=f(x)在点(e,1)处的切线方程为y-1=$\frac{1}{e}(x-e)$,
即x-ey=0;
(Ⅱ)g(x)=(x-1)f′(x)=$(x-1)•\frac{1}{x}=1-\frac{1}{x}$,
f(x)≥ag(x)在[3,+∞)上恒成立,
即lnx≥a(1-$\frac{1}{x}$)在[3,+∞)上恒成立,
也就是a≤$\frac{xlnx}{x-1}$在[3,+∞)上恒成立,
令h(x)=$\frac{xlnx}{x-1}$(x≥3),
h′(x)=$\frac{(lnx+1)(x-1)-xlnx}{(x-1)^{2}}$=$\frac{x-lnx-1}{(x-1)^{2}}$.
令t(x)=x-lnx-1,则t′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$>0,
∴t(x)在[3,+∞)上单调递增,又t(3)=2-ln3>0,
∴h′(x)>0在[3,+∞)上恒成立,
即$h(x)_{min}=h(3)=\frac{3ln3}{2}$.
∴a≤$\frac{3ln3}{2}$.
∴实数a的取值范围是(-∞,$\frac{3ln3}{2}$].
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查利用导数求函数的最值,体现了分离参数方法的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{4},\frac{π}{2})∪(π,\frac{5}{4}π)$ | B. | $(\frac{π}{4},π)$ | C. | $(\frac{π}{4},\frac{3}{4}π)∪(\frac{5π}{4},\frac{7}{4}π)$ | D. | $(\frac{π}{4},\frac{π}{2})∪(\frac{5}{4}π,\frac{3}{2}π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
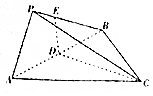 如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.
如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 1 | C. | 10 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( )
已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
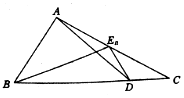 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-2 | B. | 2n-1 | C. | 3n-2 | D. | 2•3n-1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=5,b=5,A=50° | B. | a=3,b=4,A=30° | ||
| C. | a=5,b=10,A=30° | D. | a=12,b=10,A=135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 210 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com