
已知集合![]() ,若集合
,若集合![]() ,且对任意的
,且对任意的![]() ,存在
,存在![]() ,使得
,使得![]() (其中
(其中![]() ),则称集合
),则称集合![]() 为集合
为集合![]() 的一个
的一个![]() 元基底.
元基底.
(Ⅰ)分别判断下列集合![]() 是否为集合
是否为集合![]() 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
①![]() ,
,![]() ;
;
②![]() ,
,![]() .
.
(Ⅱ)若集合![]() 是集合
是集合![]() 的一个
的一个![]() 元基底,证明:
元基底,证明:![]() ;
;
(Ⅲ)若集合![]() 为集合
为集合![]() 的一个
的一个![]() 元基底,求出
元基底,求出![]() 的最小可能值,并写出当
的最小可能值,并写出当![]() 取最小值时
取最小值时![]() 的一个基底
的一个基底![]() .
.
解:(Ⅰ)①![]() 不是
不是![]() 的一个二元基底.
的一个二元基底.
理由是 ![]() ;
;
②![]() 是
是![]() 的一个二元基底.
的一个二元基底.
理由是 ![]() ,
,
![]() .21世纪教育网
.21世纪教育网
………………………………………3分
(Ⅱ)不妨设![]() ,则
,则
形如![]()
![]() 的正整数共有
的正整数共有![]() 个;
个;
形如![]()
![]() 的正整数共有
的正整数共有![]() 个;
个;
形如![]()
![]() 的正整数至多有
的正整数至多有![]() 个;
个;
形如![]()
![]() 的正整数至多有
的正整数至多有![]() 个.
个.
又集合![]() 含
含![]() 个不同的正整数,
个不同的正整数,![]() 为集合
为集合![]() 的一个
的一个![]() 元基底.
元基底.
故![]() ,即
,即![]() . ………………………………………8分
. ………………………………………8分
(Ⅲ)由(Ⅱ)可知![]() ,所以
,所以![]() .
.![]()
当![]() 时,
时,![]() ,即用基底中元素表示出的数最多重复一个. *
,即用基底中元素表示出的数最多重复一个. *
假设![]() 为
为![]() 的一个4元基底,
的一个4元基底,
不妨设![]() ,则
,则![]() .
.
当![]() 时,有
时,有![]() ,这时
,这时![]() 或
或![]() .
.
如果![]() ,则由
,则由![]() ,与结
,与结![]() 论*矛盾.
论*矛盾.
如果![]() ,则
,则![]() 或
或![]() .易知
.易知![]() 和
和![]() 都不是
都不是![]() 的4元基底,矛盾.
的4元基底,矛盾.
当![]() 时,有
时,有![]() ,这时
,这时![]() ,
,![]() ,易知
,易知![]() 不是
不是![]() 的4元基底,矛盾.
的4元基底,矛盾.
当![]() 时,有
时,有![]() ,这时
,这时![]() ,
,![]() ,易知
,易知![]() 不是
不是![]() 的4元基底,矛盾.
的4元基底,矛盾.
当![]() 时,有
时,有![]() ,
,![]() ,
,![]() ,易知
,易知![]() 不是
不是![]() 的4元基底,矛盾.
的4元基底,矛盾.
当![]() 时,有
时,有![]() ,
,![]() ,
,![]() ,易知
,易知![]() 不是
不是![]() 的4元基底,矛盾.
的4元基底,矛盾.
当![]() 时,有
时,有![]() ,
,![]() ,
,![]() ,易知
,易知![]() 不是
不是![]() 的4元基底,矛
的4元基底,矛![]() 盾.
盾.
当![]() 时,有
时,有![]() ,
,![]() ,
,![]() ,易知
,易知![]() 不是
不是![]() 的4元基底,矛盾.
的4元基底,矛盾.
当![]() 时,
时,![]() 均不可能是
均不可能是![]() 的4元基底.
的4元基底.
当![]() 时,
时,![]() 的一个基底
的一个基底![]() ;或{3,7,8,9,10};或{4,7,8,9,10}等,只要写出一个即可.
;或{3,7,8,9,10};或{4,7,8,9,10}等,只要写出一个即可.
综上,![]() 的最小可能值为5. ……………………14分
的最小可能值为5. ……………………14分


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届北京市高一第一学期期末考试数学 题型:解答题
(本小题满分14分)
已知集合 ,若集合
,若集合 ,且对任意的
,且对任意的 ,存在
,存在 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.
(Ⅰ)分别判断下列集合 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
①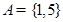 ,
, ;
;
② ,
, .
.
(Ⅱ)若集合 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: ;
;
(Ⅲ)若集合 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.
查看答案和解析>>
科目:高中数学 来源:2012届北京市海淀区高三上学期期末考试理科数学 题型:解答题
(本小题满分14分)
已知集合 ,若集合
,若集合 ,且对任意的
,且对任意的 ,存在
,存在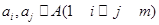 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.
(Ⅰ)分别判断下列集合 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
① ,
, ;
;
② ,
, .
.
(Ⅱ)若集合 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: ;
;
(Ⅲ)若集合 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com