Question

如果抛物线y²=px和圆（x-2）²+y²=3相交，它们在x轴上方的交点A、B，那么当p为何值时，线段AB的中点M在直线y=x上．

Answer 1

【答案】分析：先把两个方程联立求出关于点A、B和p的方程，再求出中点坐标以及直线AB的斜率，最后利用圆中垂直弦平分弦的性质来求p值即可．
解答：解：由题得p＞0．
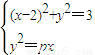
设点A，B的坐标分别为（x₁，y₁）和（x₂，y₂），圆的圆心为点C，联立⇒x²-（4-p）x+1=0，
△=（4-p）²-4＞0⇒p＞6或0＜p＜2，
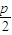
有x₁+x₂=4-p＞0⇒0＜p＜2，且线段AB的中点M的坐标为（2-，2-）．
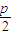
又因为k_AB=====．
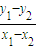
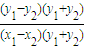
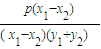
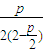
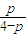
k_CM==．
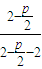
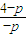
所以k_AB•k_CM=-1．即AB与CM恒垂直满足圆中垂直弦平分弦的结论
故所求   0＜p＜2．
点评：本题是对抛物线与圆的综合考查．主要用到了圆内的垂径定理．