
甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
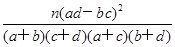 . ?
. ?| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:解答题
某学校制定学校发展规划时,对现有教师进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
| 学历 | 35岁以下 | 35至50岁 | 50岁以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 | x | 20 | y |
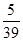 ,求x、y的值.
,求x、y的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.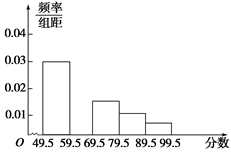
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数是多少;
(3)这两个班参赛学生的成绩的中位数应落在第几小组内.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位最近组织了一次健身活动,参加活动的职工分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的 ,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
(1)游泳组中青年人、中年人、老年人分别所占的比例.
(2)游泳组中青年人、中年人、老年人分别应抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某市民众对政府出台楼市限购令的情况,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令赞成的人数如下表:
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 非高收入族 | 高收入族 | 合计 |
| 赞成 | | | |
| 不赞成 | | | |
| 合计 | | | |
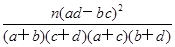
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某次测验中,有6位同学的平均成绩为75分.用 表示编号为
表示编号为 (
( )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
(1)求第6位同学的成绩 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与 有关.
有关.  是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.  日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见下表:
日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见下表:
 日均值k(微克) 日均值k(微克) | 空气质量等级 |
 | 一级 |
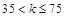 | 二级 |
 | 超标 |

 日均值作为样本,样本数据茎叶图如右图所示(十位为茎,个位为叶).
日均值作为样本,样本数据茎叶图如右图所示(十位为茎,个位为叶). 日均值的样本平均数,据此判断该月中哪个市的空气质量较好;
日均值的样本平均数,据此判断该月中哪个市的空气质量较好;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定。空气质量指数越高,代表空气污染越严重:
| 空气质量指数 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | ≥250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人,将这l6人的数学成绩编成茎叶图,如图所示.
(I)茎叶图中有一个数据污损不清(用△表示),若甲班抽出来的同学平均成绩为l22分,试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍,请将所有可能的结果列举出来,并求选出的两位同学不在同一个班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com