

分析 (1)写出该超市这两年销售量前5名的五个奶粉的销量的前五强排名;
(2)计算这5个品牌奶粉2016年所占总销量(仅指这5个品牌奶粉的总销量)的百分比,再填表;
(3)计算购买飞鹤奶粉的概率,求出X的可能取值以及概率值,求出分布列与数学期望.
解答 解:(1)该超市这两年销售量前5名的五个奶粉的销量的前五强排名是:
飞鹤奶粉,伊利奶粉,贝因美奶粉,雅士利奶粉,完达山奶粉;
(2)计算这5个品牌奶粉2016年所占总销量(仅指这5个品牌奶粉的总销量)的百分比,
将数据填入如图2饼状图中的括号内;
(3)由(2)知,购买飞鹤奶粉的概率是$\frac{1}{4}$,X的可能取值为0,1,2;
则P(X=0)=${(1-\frac{1}{4})}^{2}$=$\frac{9}{16}$,
P(X=1)=${C}_{2}^{1}$×$\frac{1}{4}$×(1-$\frac{1}{4}$)=$\frac{3}{8}$,
P(X=2)=${(\frac{1}{4})}^{2}$=$\frac{1}{16}$;
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{9}{16}$ | $\frac{3}{8}$ | $\frac{1}{16}$ |
点评 本题考查了频率分布直方图与离散型随机变量的分布列与数学期望的计算问题,是综合题.


科目:高中数学 来源: 题型:解答题
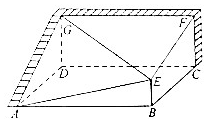 要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.
要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{41}$ | B. | 4$\sqrt{5}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com