
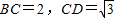 ,
,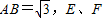 分别为AC、AD上的动点.
分别为AC、AD上的动点.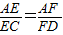 ,求证:平面BEF⊥平面ABC;
,求证:平面BEF⊥平面ABC;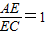 ,
,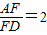 ,求平面BEF与平面BCD所成的锐二面角的大小.
,求平面BEF与平面BCD所成的锐二面角的大小.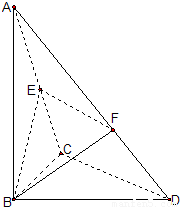
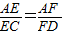 ,根据平行线分线段成比例定理,可得EF∥CD,由线面垂直的第二判定定理可得EF⊥平面ABC,再由面面垂直的判定定理,可得平面BEF⊥平面ABC;
,根据平行线分线段成比例定理,可得EF∥CD,由线面垂直的第二判定定理可得EF⊥平面ABC,再由面面垂直的判定定理,可得平面BEF⊥平面ABC;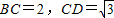 ,
,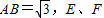 分别为AC、AD上的动点,
分别为AC、AD上的动点,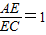 ,
,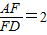 ,分别求出平面BEF与平面BCD的法向量,代入向量夹角公式,即可求出平面BEF与平面BCD所成的锐二面角的大小.
,分别求出平面BEF与平面BCD的法向量,代入向量夹角公式,即可求出平面BEF与平面BCD所成的锐二面角的大小.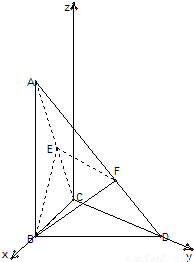 (1)∵AB⊥平面BCD,
(1)∵AB⊥平面BCD,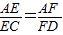 ,
,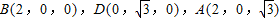 ,
,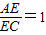 ,
,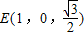 ,
,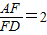 ,
,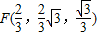
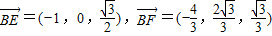 ,
,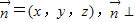 平面BEF,
平面BEF,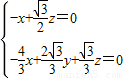 ,
,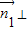 平面BCD,则
平面BCD,则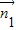 可取(0,0,1),
可取(0,0,1),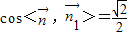 ,
,
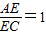 ,
,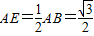 ,
,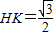 ,
,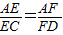 ,根据平行线分线段成比例定理,转化为EF∥CD,(2)中方法一的关键是将二面角问题转化为向量夹角问题,方法二的关键是确定∠EKH即为所求二面角的平面角.
,根据平行线分线段成比例定理,转化为EF∥CD,(2)中方法一的关键是将二面角问题转化为向量夹角问题,方法二的关键是确定∠EKH即为所求二面角的平面角. 

科目:高中数学 来源: 题型:
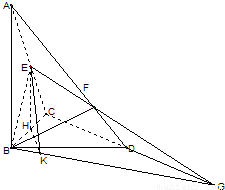
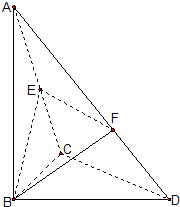 如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=2,CD=
如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=2,CD=| 3 |
| 3 |
| AE |
| EC |
| AF |
| FD |
| AE |
| EC |
| AF |
| FD |
查看答案和解析>>
科目:高中数学 来源: 题型:
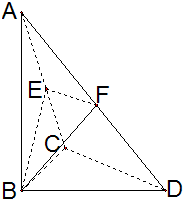 如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=CD=1,AB=
如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=CD=1,AB=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
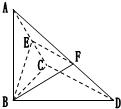 如图,已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
如图,已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且| AE |
| AC |
| AF |
| AD |
| 6 |
| 7 |
| 6 |
| 7 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市安福中学高二(上)期中数学试卷(理科)(解析版) 题型:填空题
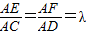 (0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .
(0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市安福中学高二(上)期中数学试卷(理科)(解析版) 题型:填空题
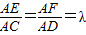 (0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .
(0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com