
如图所示,在长方体ABCD—A1B1C1D1中,AB=BC=1,BB1=2,
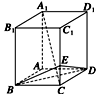
E是棱CC1上的点,且CE=![]() CC1.
CC1.
(1)求三棱锥C—BED的体积;
(2)求证:A1C⊥平面BDE.
(1)![]() (2)证明略
(2)证明略
(1)∵CE=![]() CC1=
CC1=![]() ,
,
∴VC—BDE=VE—BCD=![]() S△BCD·CE
S△BCD·CE
=![]() ×
×![]() ×1×1×
×1×1×![]() =
=![]() .
.
(2)证明 连接AC、B1C.
∵AB=BC,∴BD⊥AC.
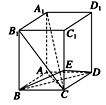 ∵A1A⊥底面ABCD,
∵A1A⊥底面ABCD,
∴BD⊥A1A.
∵A1A∩AC=A,
∴BD⊥平面A1AC.
∴BD⊥A1C.
∵tan∠BB1C=![]() =
=![]() ,
,
tan∠CBE=![]() =
=![]() ,∴∠BB1C=∠CBE.
,∴∠BB1C=∠CBE.
∵∠BB1C+∠BCB1=90°,
∴∠CBE+∠BCB1=90°,∴BE⊥B1C.
∵BE⊥A1B1,A1B1∩B1C=B1,
∴BE⊥平面A1B1C,∴BE⊥A1C.
∵BD∩BE=B,BE![]() 平面BDE,BD
平面BDE,BD![]() 平面BDE,
平面BDE,
∴A1C⊥平面BDE.


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在长方体中,AB=12,BC=6,AA′=5,分别过BC和A′D′的两个平行平面将长方体分为体积相等的三个部分,那么F′D′等于( )
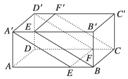
A.8 B.6
C.4 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在长方体中,AB=12,BC=6,AA′=5,分别过BC和A′D′的两个平行平面将长方体分为体积相等的三个部分,那么F′D′等于( )

A.8 B.6
C.4 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在长方体中,AB=12,BC=6,AA′=5,分别过BC和A′D′的两个平行平面将长方体分为体积相等的三个部分,那么F′D′等于( )

A.8 B.6
C.4 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com