
科目:高中数学 来源: 题型:填空题
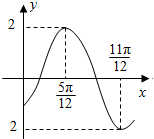 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
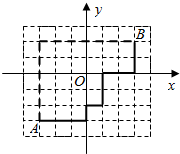 现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com