
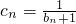 ,记Tn=c1c2+2c2c3+22c3c4+…+2n-1cncn+1,比较Tn与
,记Tn=c1c2+2c2c3+22c3c4+…+2n-1cncn+1,比较Tn与 的大小.
的大小.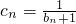 =
=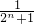 Tn=c1c2+2c2c3+22c3c4+…+2n-1cncn+1
Tn=c1c2+2c2c3+22c3c4+…+2n-1cncn+1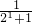 ×
×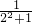 +2×
+2×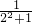 ×
×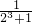 +…+2n-1×
+…+2n-1×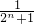 ×
×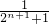
 ×(
×(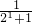 -
-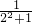 )+
)+ ×(
×(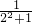 -
-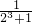 )+…+
)+…+ ×(
×(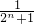 -
-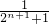 )
) ×(
×(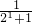 -
-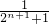 )
) -
-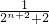 ∴
∴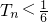
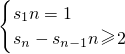 ,由已知可得an+1=2an-2n+2,转化构造数列{bn}.研究其性质.
,由已知可得an+1=2an-2n+2,转化构造数列{bn}.研究其性质.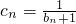 =
=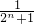 ,∴2 n-1 cncn+1=
,∴2 n-1 cncn+1= ×(
×(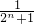 -
-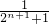 ),Tn可求其表达式,再进行证明.
),Tn可求其表达式,再进行证明.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:
| 1 |
| an-n |
| 37 |
| 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| Sn |
| n |
| 1 |
| anan+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| g |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 11 |
| 2 |
| 6 |
| (2an-11)(2bn-1) |
| k |
| 57 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com