已知直线l1:(1+λ)x+y+2λ+1=0(λ∈R),直线l2过点A(-3,2),B(-1,3).
(1)若l1⊥l2,求直线l1的方程;
(2)若直线l1和线段AB有交点,求λ的取值范围.
解:(1)直线l
2的斜率为
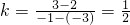
,
∵l
1⊥l
2,
所以直线l
1的斜率为k
1=-2?-(1+λ)=-2?λ=1
故直线l
1的方程是:2x+y+3=0;
(2)由题意得,直线l
1:(1+λ)x+y+2λ+1=0(λ∈R),即λ(x+2)+(x+y+1)=0,
因此直线l
1恒过定点P(-2,1),
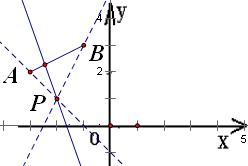
∵PA的斜率为
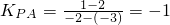
,
PB的斜率为

,
且直线l
1和线段AB有交点,
∴直线l
1的斜率在小于或等于-1,或大于或等于

的范围内
即-(1+λ)≤-1或-(1+λ)≥2
解之得λ≥0或λ≤-3.
分析:(1)先根据经过两点的直线的斜率公式,计算出直线l
2的斜率,再根据l
1⊥l
2,垂直直线的斜率之积等于-1,得到直线l
1的斜率,从而求出λ的值,得到直线l
1的方程;
(2)化简直线l
1的方程为:λ(x+2)+(x+y+1)=0,得到直线l
1恒过定点P(-2,1),再分别求出PA、PB的斜率,根据直线l
1和线段AB有交点,通过观察直线l
1的倾斜角的变化,得到直线l
1的斜率的取值范围,最终得到实数λ的取值范围.
点评:本题借助于两条直线的位置关系和动直线与线段有交点的讨论,着重考查了直线的基本量和基本形式,以及直线的相互关系等知识点,属于基础题.

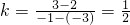 ,
,
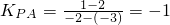 ,
, ,
, 的范围内
的范围内
