
 .
. =6的概率;
=6的概率; 的分布列和期望.
的分布列和期望.科目:高中数学 来源:不详 题型:解答题
 其中
其中 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).  “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率 与事件
与事件 “在四次试验中,
“在四次试验中, ;
; ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
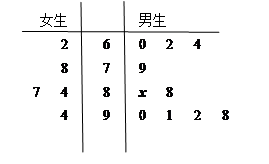
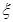 ,求
,求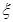 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
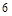 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为 ).
). ,求随机变量
,求随机变量 的分布列与期望.
的分布列与期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;| 号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 品种A | 101 | 97 | 92 | 103 | 91 | 100 | 110 | 106 |
| 品种B | 115 | 107 | 112 | 108 | 111 | 120 | 110 | 113 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、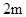 、
、 的钢管各
的钢管各 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根. 时,记事件
时,记事件 {抽取的
{抽取的 根钢管中恰有
根钢管中恰有 根长度相等},求
根长度相等},求 ;
; 时,若用
时,若用 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求 的分布列;
的分布列; ,
, ,求实数
,求实数 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com