
在一个花瓶中装有6枝鲜花,其中3枝山茶花,2枝杜鹃花和1枝君子兰,从中任取2枝鲜花.
(Ⅰ)求恰有一枝山茶花的概率;
(Ⅱ)求没有君子兰的概率.
解:设3枝山茶花为a、b、c,2枝杜鹃花为m、n,1枝君子兰为d. 则从6枝鲜花中任取2枝的基本事件有: (a,b)、(a,c)、(a,d)、(a,m)、(a,n)、(b,c)、(b,d)、(b,m)、(b,n)、(c,d)、(c,m)、(c,n)、(d,m)、(d,n)、(m,n) 共15种.
(Ⅰ)其中恰有一枝山茶花的基本事件有: (a,d)、(a,m)、(a,n)、(b,d)、(b,m)、(b,n)、(c,d)、(c,m)、(c,n)共9种.所以恰有一枝山茶花的概率为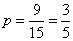 .
.
(Ⅱ)其中没有君子兰的基本事件有:(a,b)、(a,c)、(a,m)、(a,n)、(b,c)、(b,m)、(b,n)、(c,m)、(c,n)、(m,n) 共10种.所以没有君子兰的概率为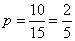 .················· 1
.················· 1


科目:高中数学 来源: 题型:
10名工人某天生产同一种零件,生产的件数是15,17,14,10,15,17,17,16,14,12.设其平均数为a,中位数为b,众数为c,则有
(A)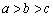 (B)
(B)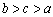 (C)
(C)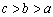 (D)
(D)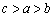
查看答案和解析>>
科目:高中数学 来源: 题型:
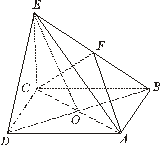
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
(Ⅰ) 求证:DE∥平面ACF;
(Ⅱ)若AB=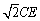 ,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出
,在线段EO上是否存在点G,使CG⊥平面BDE?若存在,求出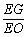 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数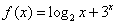 ,正实数
,正实数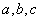 成公差为正数的等差数列,且满足
成公差为正数的等差数列,且满足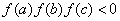 ,且实数
,且实数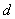 是函数
是函数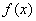 的一个零点。给出下列四个不等式:其中有可能成立的不等式有( )①
的一个零点。给出下列四个不等式:其中有可能成立的不等式有( )①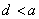 ;②
;②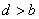 ;③
;③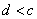 ;④
;④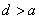 .
.
A ①②③④ B ②③④ C ①②③ D ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com