
如图,已知,在空间四边形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若![]() ,求几何体
,求几何体![]() 的体积;
的体积;
(3)若![]() 为△
为△![]() 的重心,试在线段
的重心,试在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() ∥平面
∥平面![]() .
.
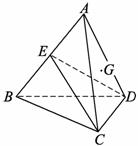
(1) 证明:∵BC=AC,E为AB的中点,∴AB⊥CE.
又∵AD=BD,E为AB的中点∴AB⊥DE. ∵![]()
∴AB⊥平面DCE∵AB![]() 平面ABC,∴平面CDE⊥平面ABC.
平面ABC,∴平面CDE⊥平面ABC.
(2)∵在△BDC中,DC=3,BC=5,BD=4,∴CD⊥BD,在△ADC中,DC=3,AD=BD=4,AC=BC=5,∴CD⊥AD,
∵![]() ∴CD⊥平面ABD.所以线段CD的长是三棱锥C-ABD的高。又在△ADB中,DE=
∴CD⊥平面ABD.所以线段CD的长是三棱锥C-ABD的高。又在△ADB中,DE=![]() ∴VC-ABD=
∴VC-ABD=![]() (3)在AB上取一点F,使AF=2FE,则可得GF∥平面CDE 取DC的中点H,连AH、EH∵G为△ADC的重心,∴G在AH上,且AG=2GH,连FG,则FG∥EH又∵FG
(3)在AB上取一点F,使AF=2FE,则可得GF∥平面CDE 取DC的中点H,连AH、EH∵G为△ADC的重心,∴G在AH上,且AG=2GH,连FG,则FG∥EH又∵FG![]() 平面CDE, EH
平面CDE, EH![]() 平面CDE,∴GF∥平面CDE
平面CDE,∴GF∥平面CDE


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
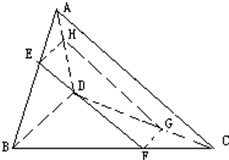 如图,要在呈空间四边形的支架上安装一块矩形的太阳能吸光板(图中EFGH),矩形的四个顶点分别在空间四边形ABCD的边上.已知AC=a,BD=b,试问:E、F、G、H分别在什么位置时,吸光板的面积最大?
如图,要在呈空间四边形的支架上安装一块矩形的太阳能吸光板(图中EFGH),矩形的四个顶点分别在空间四边形ABCD的边上.已知AC=a,BD=b,试问:E、F、G、H分别在什么位置时,吸光板的面积最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com