
��2012�߿����������21������С������13�֣�
��ֱ������ϵxOy�У�����C1�ĵ����C2����x-5��2��y2=9�⣬�Ҷ�C1������һ��M��M��ֱ��x=��2�ľ�����ڸõ���ԲC2�ϵ�ľ������Сֵ.
����������C1�ķ��̣�
������P(x0,y0)��y0�١�3��ΪԲC2��һ�㣬��P��ԲC2���������ߣ��ֱ�������C1�ཻ�ڵ�A��B��C��D.֤������P��ֱ��x=��4���˶�ʱ���ĵ�A��B��C��D��������֮��Ϊ��ֵ.
���ⷨ1 ����M������Ϊ![]() ������֪��
������֪��
![]() ��
��
��֪Բ![]() �ϵĵ�λ��ֱ��
�ϵĵ�λ��ֱ��![]() ���Ҳ�.����
���Ҳ�.����![]() ������
������
![]() .
.
���������![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
�ⷨ2 ��������֪������![]() ������һ��M��Բ��
������һ��M��Բ��![]()
![]() �ľ����������ֱ��
�ľ����������ֱ��![]() �ľ��룬��ˣ�����
�ľ��룬��ˣ�����![]() ����
����![]() Ϊ���㣬ֱ��
Ϊ���㣬ֱ��![]() Ϊ�ߵ������ߣ����䷽��Ϊ
Ϊ�ߵ������ߣ����䷽��Ϊ![]() .
.
������P��ֱ��![]() ���˶�ʱ��P������Ϊ
���˶�ʱ��P������Ϊ![]() ����
����![]() �����P����Բ
�����P����Բ
![]() ���е�ֱ�ߵ�б��
���е�ֱ�ߵ�б��![]() �����Ҳ�Ϊ0��ÿ�����߶������������������㣬���߷���Ϊ
�����Ҳ�Ϊ0��ÿ�����߶������������������㣬���߷���Ϊ![]() .����
.����
![]()
������
![]() ��
��
���P��������������![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ����
����![]() �Ƿ��̢ٵ�����ʵ������
�Ƿ��̢ٵ�����ʵ������
![]() ��
��
��![]() ��
��![]() ��
��
���ĵ�A,B,C,D��������ֱ�Ϊ![]() �����Ƿ��̢۵�����ʵ��������
�����Ƿ��̢۵�����ʵ��������
![]() ��
��
ͬ���ɵ�
![]() ��
��
�����ɢڣ��ܣ�����ʽ��
![]()
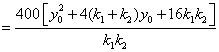
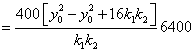 .
.
���ԣ���P��ֱ��![]() ���˶�ʱ���ĵ�A��B��C��D��������֮��Ϊ��ֵ6400.
���˶�ʱ���ĵ�A��B��C��D��������֮��Ϊ��ֵ6400.
�����������⿼�������뷽�̡�ֱ�������ߵ�λ�ù�ϵ�����������������������ν��˼�롢�����뷽��˼�����ѧ˼�뷽��.��һ����ֱ�ӷ����巨������ߵķ��̣��ڶ���������߷��̣���ֱ�������߷�����������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�![]() �ĵ�������֮��Ϊ��ֵ�����֡��������˼��.
�ĵ�������֮��Ϊ��ֵ�����֡��������˼��.


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2012�߿�����������3�������ʵ��k��ֱ��![]() ��Բ
��Բ![]() ��λ�ù�ϵһ����
��λ�ù�ϵһ����
��1�� ���� B.���� C.�ཻ��ֱ�߲���Բ�� D.�ཻ��ֱ�߹�Բ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2012�߿������㽭��3����a��R ����a��1���ǡ�ֱ��l1��ax+2y=0��ֱ��l2 ��x+(a+1)y+4=0ƽ�� ��
A ��ֲ���Ҫ���� ������B ��Ҫ���������
C ��ֱ�Ҫ���� ����������D �Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2012�߿�����������4����֪Բ![]() ��
��![]() ����
����![]() ��ֱ�ߣ��� ��
��ֱ�ߣ��� ��
A.![]() ��
��![]() �ཻ B.
�ཻ B. ![]() ��
��![]() ���� C.
���� C.![]() ��
��![]() ���� D. ��������ѡ����п���
���� D. ��������ѡ����п���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2012�߿����������8����![]() ����ֱ��
����ֱ��![]() ��Բ
��Բ![]() ���У���m+n��ȡֵ��Χ��
���У���m+n��ȡֵ��Χ��
��A��![]() ��B��
��B��![]()
��C��![]() ��D��
��D��![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com